Elasticidades: elasticidad de la demanda y elasticidad del ingreso.
Objetivo
EL objetivo de este blog es de brindar información útil para todo el mundo.
La elasticidad de la demanda
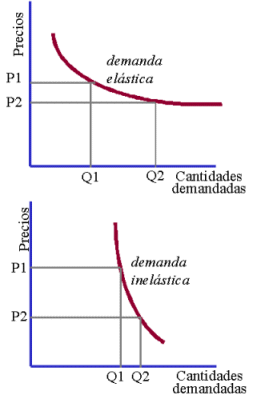
Hay algunos bienes cuya demanda es muy sensible al precio, pequeñas variaciones en su precio provocan grandes variaciones en la cantidad demandada. Se dice de ellos que tienen demanda elástica. Los bienes que, por el contrario, son poco sensibles al precio son los de demanda inelástica o rígida. En éstos pueden producirse grandes variaciones en los precios sin que los consumidores varíen las cantidades que demandan. El caso intermedio se llama de elasticidad unitaria.
La elasticidad de la demanda se mide calculando el porcentaje en que varía la cantidad demandada de un bien cuando su precio varía en un uno por ciento. Si el resultado de la operación es mayor que uno, la demanda de ese bien es elástica; si el resultado está entre cero y uno, su demanda es inelástica.
Los factores que influyen en que la demanda de un bien sea más o menos elástica son:
1) Tipo de necesidades que satisface el bien. Si el bien es de primera necesidad la demanda es inelástica, se adquiere sea cual sea el precio; en cambio si el bien es de lujo la demanda será elástica ya que si el precio aumenta un poco muchos consumidores podrán prescindir de él.
2) Existencia de bienes sustitutivos. Si existen buenos sustitutos la demanda del bien será muy elástica. Por ejemplo, un pequeño aumento en el precio del aceite de oliva puede provocar que un gran número de amas de casa se decida por usar el de girasol.
3) Importancia del bien en términos de coste. Si el gasto en ese bien supone un porcentaje muy pequeño de la renta de los individuos, su demanda será inelástica. Por ejemplo, el lápiz. Las variaciones en su precio influyen muy poco en las decisiones de los consumidores que desean adquirirlos.
4) El paso del tiempo. Para casi todos los bienes, cuanto mayor sea el período de tiempo considerado mayor será la elasticidad de la demanda. Puede ser que al aumentar el precio de la gasolina, su consumo no varíe mucho, pero al pasar el tiempo podrá ser substituida en algunos de sus usos por el carbón, en otros usos por el alcohol, de forma que la disminución en la demanda sólo se nota cuando pasa el tiempo.
5) El precio. finalmente hay que tener en cuenta que la elasticidad de la demanda no es la misma a lo largo de toda la curva. Es posible que para precios altos la demanda sea menos elástica que cuando los precios son más bajos o al revés, dependiendo del producto de que se trate.
Hay diferentes clases de elasticidad. El fenómeno que hemos estado analizando bajo el nombre de "elasticidad" a secas, podríamos haberlo llamado con mayor propiedad elasticidad-precio ya que se trataba de medir la sensibilidad de la demanda a las variaciones en los precios. Pero la demanda puede ser también más o menos sensible a otros factores. Llamaremos elasticidad-renta a la medida de la sensibilidad de la demanda de un bien a las variaciones en la renta del consumidor. Llamaremos elasticidad cruzada a la medida de la sensibilidad de la demanda de un bien a las variaciones en el precio de otros bienes.

Mercado campesino en Honduras |
Según vimos antes, cuando la renta de un individuo aumenta, su consumo de todos los bienes aumentará también. Sin embargo eso no es siempre cierto. Hay algunos bienes, los llamados bienes inferiores, que se caracterizan por el hecho de que al aumentar la renta de los individuos disminuye el consumo de ellos. El ejemplo clásico es el de las patatas o, en general, el de los alimentos ricos en féculas. Conforme aumenta la renta de los individuos y de las sociedades, estos alimentos son substituidos por otros más ricos en proteínas, la carne, por ejemplo. Hay otros bienes, por el contrario, cuyo consumo aumenta más que proporcionalmente al aumentar las rentas. Son los bienes de lujo.
Para medir la sensibilidad de los bienes a las variaciones en la renta de los individuos se utiliza el concepto de elasticidad-renta: porcentaje en que varía la cantidad demandada de un bien cuando la renta del consumidor varía en un uno por ciento. En el caso de los bienes inferiores, la elasticidad-renta es negativa ya que el aumento de ésta provoca la contracción de la demanda de aquellos. La elasticidad-renta de los bienes de lujo es muy alta ya que las variaciones en la renta provocan grandes variaciones en la cantidad demandada. Los bienes de primera necesidad, a diferencia de los bienes inferiores, tienen la elasticidad-renta de la demanda positiva pero muy pequeña, en otras palabras, su demanda es inelástica con respecto a la renta. Finalmente, los bienes normales mostrarán una elasticidad-renta unitaria, es decir, su demanda aumentará aproximadamente en la misma proporción en que lo haga la renta de los individuos.
Las relaciones que existan entre bienes permiten otra forma de clasificación. Se llaman bienes complementarios a los que son consumidos conjuntamente: los coches y la gasolina, los canarios y las jaulas. La peculiaridad de estos bienes es que cuando aumenta el precio de uno disminuye la cantidad demandada del otro. El fenómeno opuesto puede observarse en el caso de los bienes sustitutivos o sustituibles, los que pueden utilizarse de forma alternativa: el aceite de oliva y el de girasol. En este caso el aumento del precio de uno provoca el aumento de la cantidad demandada del otro.
Para medir la sensibilidad de la demanda de un bien a las variaciones en el precio de otro se utiliza la elasticidad cruzada: porcentaje en que varía la cantidad demandada de un bien cuando el precio de otro varía en un uno por ciento. La elasticidad cruzada será positiva si las variaciones en el precio y en la cantidad demandada van en el mismo sentido, es decir, en el caso de los bienes sustitutivos. Como el sentido del cambio es diferente entre el precio y la demanda de los bienes complementarios, su elasticidad cruzada será negativa.
Bibliografía: http://www.eumed.net/cursecon/4/elasticidad-demanda.htm
.png)

 .
. que es continua en un intervalo abierto
que es continua en un intervalo abierto  que contiene a
que contiene a  puede clasificarse como sigue."
puede clasificarse como sigue." cambia de positiva a negativa en
cambia de positiva a negativa en  .
.








